エラストテネス の ふるい 116975

 このことが地球の大きさを調べるカギとなることに気づいたエラストテネスは、井戸の代わりに高い塔を建てて影を測りました。 エラトステネスは、塔の高さを知っていますし、影の長さもわかります。これより、上の図の角度\(\alpha\)がわかります（下の図参考）。 \(\alpha\)の角度は 今日は、2 以上 n 以下の自然数の中から素数を抽出（素数以外を排除）する C によるアルゴリズムについてです。まず、「自然数 p ( > 1 ) が 1 と p の他に正の約数を持たない場合、p を素数という。」です。そして、簡単に言うと、自然数の配列をふるいに見立てて素数以外を排除して 単純にエラトステネスの定義にしたがって、ふるいにかけたのみの code です。 1〜100までの素数の場合には 7 を除いた 7 の倍数は素数ではないとしてふるいにかけると全ての素数が出てきます。 出力後の結果は左の様になります。（最も上にある2, 3が切れてしまっています） また、

エラトステネスの篩のやり方やその計算量とは 素数を発見しよう 遊ぶ数学

エラストテネス の ふるい

エラストテネス の ふるい- 一応エラストテネスのふるいのやり方は聞きました。 そのやり方が一番適当かなと思い、私はプログラムを組んでいるのですが、なかなか出来ない状態です。^^； 通報する お礼日時： 1403 No4 回答者： Wendy02; エラトステネスの篩は指定された整数以下の全ての素数を発見するための単純なアルゴリズムで、 以下のステップからなります。 ステップ 1 探索リストに2からxまでの整数を昇順で入れる ステップ 2 探索リストの先頭の数を素数リストに移動し、その倍数を探索リストから篩い落とす

エラトステネスの篩 鋼霊的備忘録

Eratosthenesのふるいで素数を見つける(もともとこの配列を準備するには良い方法がありますか?) (9) 注：下記のバージョン2では、Sag of Eratosthenesを使用しています。 私が最初に尋ねたものに役立ついくつかの答えがあります。 私は、Sag of Eratosthenesメソッドをエラトステネス (Eratosthenēs) 古代ギリシアの数学者、天文学者、地理学者。 素数の選別法「エラトステネスの篩 (ふるい) 」を発見。 また、はじめて赤道の周囲を測量し、約四万五〇〇〇キロメートルと算出した。 主著「地理学」三巻。 （ 前二七五頃 記載の手順にそって冗長的に書いたコードです。ふるい処理の途中経過を出力しています。 In 2 # nまでの素数（エラトステネスのふるい） n = 100 A = list (range (2, n 1)) # 2～nまでの素数候補の集合リスト sqrt_n = n ** (1 / 2) # √n print ('素数候補') print (A) idx = 0 while True p = A idx # リストidx番目の素数

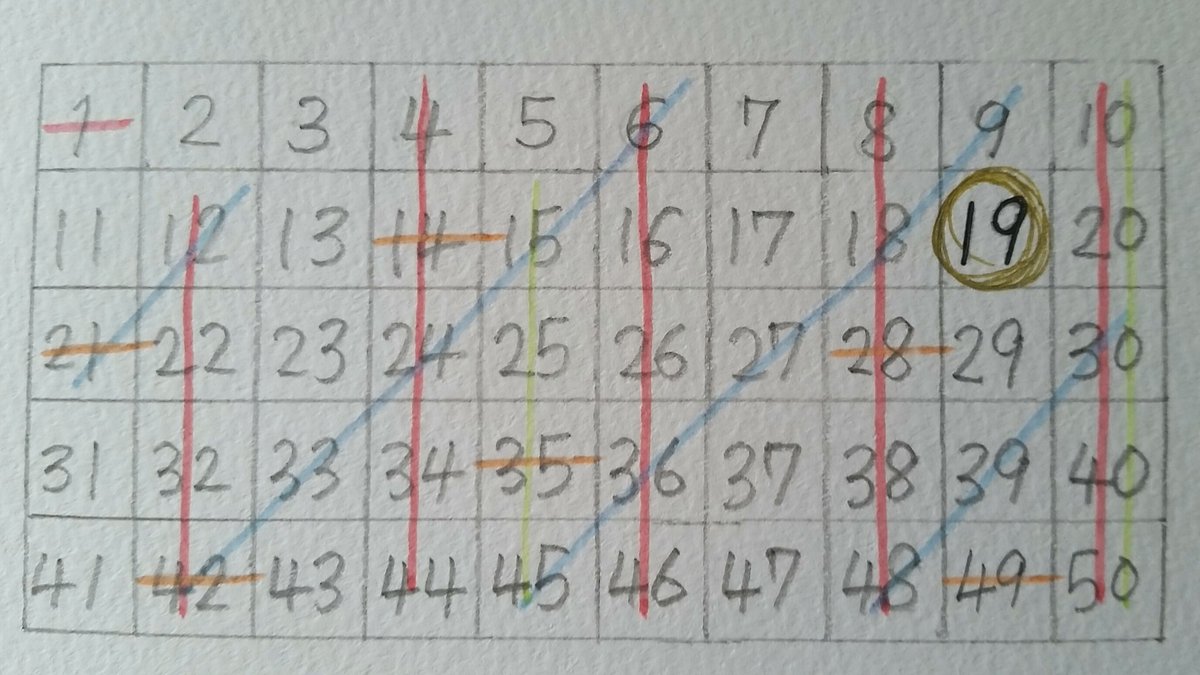
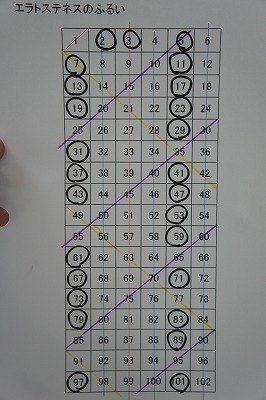
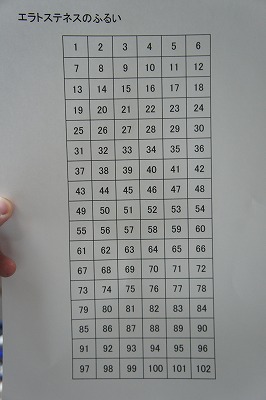
Void set_f(int i, int max) { int j;エラトステネスのふるいのやり方 今回は $1$ ～ $100$ までの素数をすべて見つけてみよう。 1．$1$ ～ $100$ までの数をすべて書き記す。 2．$1$ は素数ではないので、赤線で消す。 3．$2$ に青い $〇$ をつけ、$2$ で割り切れるものすべてを赤線で消す。 4．これを $\sqrt{100}=10$ まで繰りエラトステネスの方法は「地球が球である」という仮定のもとに行われています。 実際には地球は回転楕円体に近い形です。 シエネとアレキサンドリア間の距離も正確とはいえません。 ほかにも正確でない点がいくつかあり，この方法で計算された地球

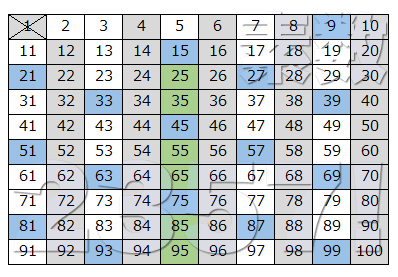
前回の isPrime() は1つの数値が素数かどうかを調べる方法だったが、今回の「エラトステネスの篩(ふるい)」は素数かどうかの一覧のような感じのもの。Wikipedia にも書いてあるように、コンピュータがある以前からあるアルゴリズムである。「ユークリッドの互除法」に並んで最古のアルゴリズム エラトステネスのふるいのアルゴリズムをみていきます。 100以下の素数を探すことにします。 ステップ1 1番目の素数2に対して、2より大きな2の倍数4,6,8,10,12,,100を消します。 ステップ2 1番目の素数2より次に大きな数を残った数の中から探します。それが2番目の素数3です。 残った数のエラトステネスが考案した 素数 検出法。 その方法は，合成数を順次 ふるい にかけるように落して，任意の正の 整数 をこえない素数を見出すことにある。 まず1は素数でないから落す。 次に2と N の間にあるすべての正の整数を大きさの順に並べる。

Set0gut1 Scratchでエラトステネスの篩 1000以下の素数を全て求める をやってみました 文法ミスが発生しない点と ブロックの内外が分かりやすい点は良さそう でも内容的にややこしい部分が楽になるかっていうと そこは特に違いがない それはそう

Mokumokuprimenumber

 2エラストテネスのふるい 教科書などで見たことはあると思います． なんの役に立つの？ と思った方も多いと思いますが，素数を列挙する計算方法としては有用です． Wikipediaの記事がアニメーション画像付きで分かりやすいので，詳細はリンク先を見て C言語でもやってみました（Ruby版）。 ※注意 この実装はまだ未熟なので、下の modify された実装を見て下さい。（17/7/4） #include int a = {0}; さっきはタイムアウトしていたプログラムが、エラストテネスの篩のおかげで非常に高速に動作するようになりましたね！ 素数を数える：一億以下の場合 しかし、素数の範囲をさらに拡大してn = 100,000,000にしてみると、タイムアウトしてしまいました。 これをさらに高速化するには

Python でエラトステネスの篩を使って素数のリストを作る 民主主義に乾杯

雑学数学 素数を見つける方法 エラトステネスの篩 ふるい で100までにある素数を調べてみよう Youtube

 エラトステネスの篩 in C C More than 5 years have passed since last update Project Eulerの素数を扱う問題で必要になったので、エラトステネスの篩を実装してみた。 実装した関数 sieve は、上限 max までの数の中で素数であるものを探し、対応する IsPrime の要素を trueエラトステネスのふるい 素数の個数 2，3，5，7，11，13，17，19，23，29，・・・・・・・・・・ 素数（そすう）はいったいどれくらいあるのでしょうか。 （素数って何か知らない人は＜お勉強＞の「素数と素因数分解」を見てね。） じつは、無限に多くあることが古くから知られていますCork81 score 7 for を使って 1から100までの連続する整数値を画面に表示します。 ただし、素数でないものは表示しないでください。以下のルールについて調べること

エラトステネスの篩 Wikipedia

センターまで エラストテネスのふるい あと日 ｚ会東大進学教室便り

/08/ 本記事ではエラトステネスの篩（ふるい）をPythonで実装していきます。実際に問題を解きながらエラトステネスの篩の動きを確認していきましょう。 エラトステネスの篩とは 例題 問題文 制約 実装 まとめ エラトステネスの篩とは エラトステネスは古代ギリシャの学者で、数学や天文学に3「エラストテネスのふるい」を使う。 素数の判定には「エラストテネスのふるい」という方法があります。 数列から素数の倍数を消してゆき、素数だけを残す方法です。 例として90以下の素数を書き エラストテネスのふるい（篩）の使い方がわかる5ステップ 5ステップで素数を求めていくよ。 自然数をかく はじめらへんの素数に をつける 「1」を斜線で消す 「 をつけた素数の倍数」を斜線で消す 残ったやつが「素数」 例として、 1から100までの素数

エラトステネスのふるい Inamori S Diary

エラトステネスはどうやって地球の大きさを知ったのか 00年前とは思えぬ脅威の精度 数学の面白いこと 役に立つことをまとめたサイト

 この記事では「 Python入門素数の生成・判定プログラムを実装してみよう！ 」といった内容について、誰でも理解できるように解説します。この記事を読めば、あなたの悩みが解決するだけじゃなく、新たな気付きも発見できることでしょう。お悩みの方はぜひご一読ください。 何も考えず、愚直にエラトステネスのふるいを実装した場合。 配列をラベル付けする数字が0から始まるのに対して、配列の中の数字は1から始まっていると考えている。 その食い違いに解消のためにi1になっている所がある。 Pythonエラトステネスの篩というアルゴリズムを使えば素数を簡単に探すことができます。 そのアルゴリズムをPythonで実装してみました。 ソースコードは以下のとおりです。 View the code on Gis

Newみんなの算数講座49 エラトステネスのふるい 中学受験の算数知恵宝庫

整数 発展問題１ 解答 学ぶ 教える Com

 紀元前3世紀、ヘレニズム時代のエジプトで活躍した人物、 エラトステネス。 ギリシャの都市に誕生した彼は、エジプトのファラオの命により、当時最高峰の英知が集結していた図書館の館長を長年にわたって務めました。 科学的な視点を用いてあらゆる学問に精通していた彼は、やが/09/19 pythonにてエラトステネスのふるいを実装する 解決済 回答 1 投稿 1029 ・編集 1036 評価 ;For ( j =

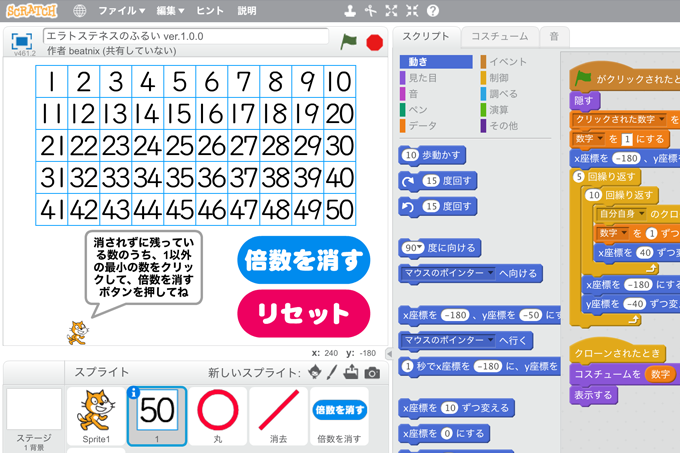
既存の教科でプログラミング授業 小学5年生 算数 エラトステネスのふるい コドモとアプリ

エラトステネスのふるい 雑多なメモ置き場

素数の求め方 エラストテネスの篩 ふるい がわかる5ステップ Qikeru 学びを楽しくわかりやすく

エラトステネスの篩 雑学のソムリエ

Python入門 素数の生成 判定プログラムを実装してみよう 侍エンジニアブログ

サンダラムの篩 Wikipedia

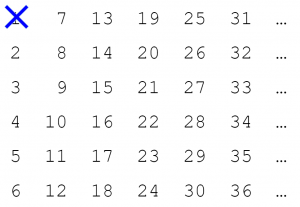
19年の素数日 エラトステネスのふるい 情報科 いっぽ まえへ

Scratch2 0 素数を見つける エラトステネスのふるい Youtube

素数をすばやく見つける方法 エラトステネスのふるい 数学の面白いこと 役に立つことをまとめたサイト

素数プログラミング エラトステネスのふるい Necoffeeのにっき

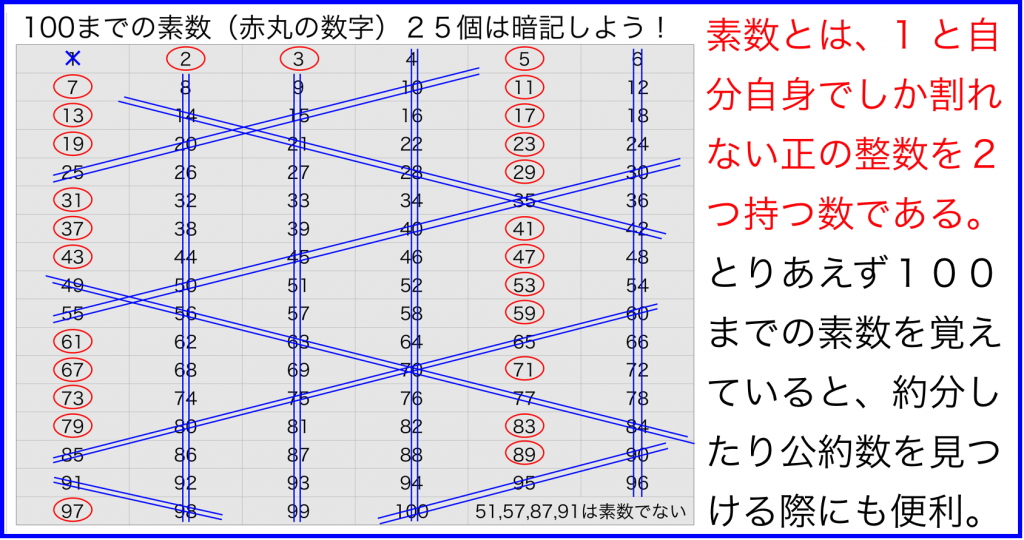
横田式100までの素数を見つける方法 エラトステネスの篩 ネットビジネス アナリスト横田秀珠

センターまで エラストテネスのふるい あと日 ｚ会東大進学教室便り

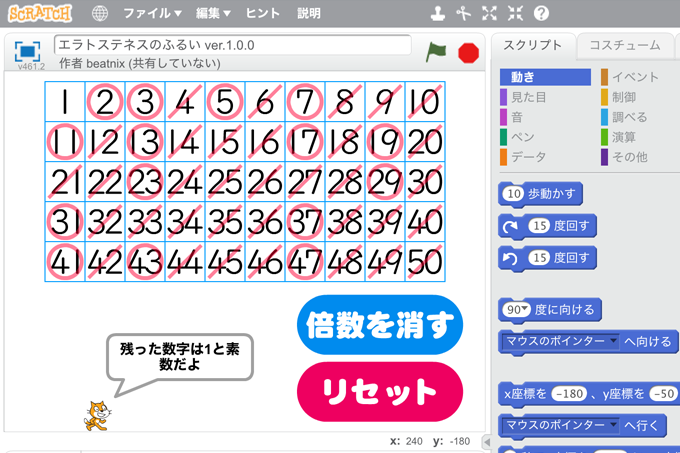
既存の教科でプログラミング授業 小学5年生 算数 エラトステネスのふるい コドモとアプリ

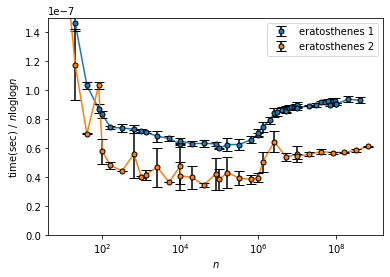
エラトステネスの篩の計算量を実験で確認する Qiita

素数生成プログラム エラトステネスのふるい を実装 Pythonで数学を学ぼう 第7回 空間情報クラブ 株式会社インフォマティクス

エラトステネスのふるい Fortran66のブログ

第18回 選べないのに見える数 後編 数学ガールの秘密ノート 結城浩 Cakes ケイクス

素数生成プログラム エラトステネスのふるい を実装 Pythonで数学を学ぼう 第7回 空間情報クラブ 株式会社インフォマティクス

エラトステネスのふるい 100までの素数 で合ってますか エラトス 中学校 教えて Goo

エラトステネスの篩 アルゴリズムビジュアル大事典

エラトステネスの篩のやり方やその計算量とは 素数を発見しよう 遊ぶ数学

100までの素数を調べる エラトステネスのふるいの使い方を解説 たぬぬ塾 中学校の先生たち

エラトステネスの篩 ふるい って名前めっちゃカッコイイ 凡庸なる人のブログ

エラトステネスのふるいとその計算量 高校数学の美しい物語

エラトステネスのふるい 素数を見つける方法

エラストテネスの篩

第11回 コンピュータのスピードを比較してみよう 日経クロステック Xtech

素数 エラトステネスのふるい

素数2357 1はなぜ素数ではないのか

エラトステネスの篩の小噺 Motsu Xe 競プロのhogeやfuga

エラストテネスのふるい Twitter Search

素数の求め方 数学の星

19年の素数日 エラトステネスのふるい 情報科 いっぽ まえへ

Newみんなの算数講座49 エラトステネスのふるい 中学受験の算数知恵宝庫

素数の求め方 数学の星

素数をすばやく見つける方法 エラトステネスのふるい 数学の面白いこと 役に立つことをまとめたサイト

素数をすばやく見つける方法 エラトステネスのふるい 数学の面白いこと 役に立つことをまとめたサイト

エラトステネスのふるい 高校生 数学のノート Clear

素数とは Fukusukeの数学めも

奇数 図表 素数 エラトステネスの篩 線 の画像素材 写真素材ならイメージナビ

かず５年 1010

一週間で身につくアルゴリズムとデータ構造 入門編6日目 アルゴリズムの例

エラトステネスの篩 鋼霊的備忘録

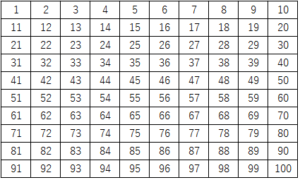
6の数表でエラトステネスのふるい 授業がんばりmath

9 16 16 1 16 Descubre Como Resolverlo En Qanda

エラトステネスの篩を用いた素数判定 19 05 08

ほぼc だけのぶろぐ

素因数分解の解説お願いします 習ったのですが やり方を忘れてしまいました Clear

既存の教科でプログラミング授業 小学5年生 算数 エラトステネスのふるい コドモとアプリ

エラトステネスの篩のやり方やその計算量とは 素数を発見しよう 遊ぶ数学

素数の求め方 エラストテネスの篩 ふるい がわかる5ステップ Qikeru 学びを楽しくわかりやすく

エラトステネスのふるい レッチワース ブログ

エラトステネス Wikipedia

エラトステネスの篩 アルゴリズムビジュアル大事典

素数アニメーション エラトステネスのふるい Youtube

エラトステネスは地球の大きさを測った 古代の学者が着目した方法とは ココが知りたい話題の小ネタ

エラトステネスのふるいについて C言語の課題でエラトステネスの Yahoo 知恵袋

エラトステネスの篩 アルゴリズムビジュアル大事典

かず５年 1010

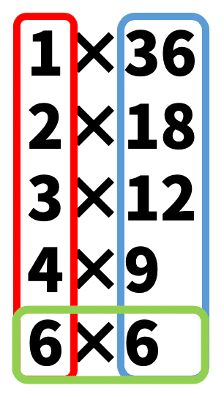
エラトステネスの篩 ふるい で100までにある素数を見つける方法 Math Channel Note

素数をすばやく見つける方法 エラトステネスのふるい 数学の面白いこと 役に立つことをまとめたサイト

エラトステネスの篩 ふるい で100までにある素数を見つける方法 Math Channel Note

エラトステネスの篩で調べる 素数判定の上限と平方根の関係性 Szarny Io

素数とエラトステネスのふるい

山岡の地理b準備室 エラトステネスの篩 ふるい

今更聞けないエラトステネスのふるい Qiita

自然数をエラトステネスのふるいにかけると 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles

エラトステネスの篩で1000までの素数を探してみる R For Radio

素数とエラトステネスのふるい

素数 を数えて落ちつくんだ 素数の無限性 の証明する エラトステネスの篩 ユークリッドの証明 エルンスト クンマーの証明 をやさしく解説してみた

Haskellでエラトステネスの篩 Blanktar

素数とは Fukusukeの数学めも

素数とエラトステネスのふるい

エラトステネスのふるい 素数を見つける方法

一週間で身につくアルゴリズムとデータ構造 入門編6日目 アルゴリズムの例

算楽塾 エラトステネスのふるいー数学者たちを虜にする魅惑の素数 Facebook

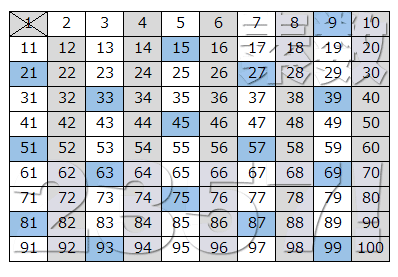
素数2357 1はなぜ素数ではないのか

エラトステネスの篩 ふるい で100までにある素数を見つける方法 Math Channel Note

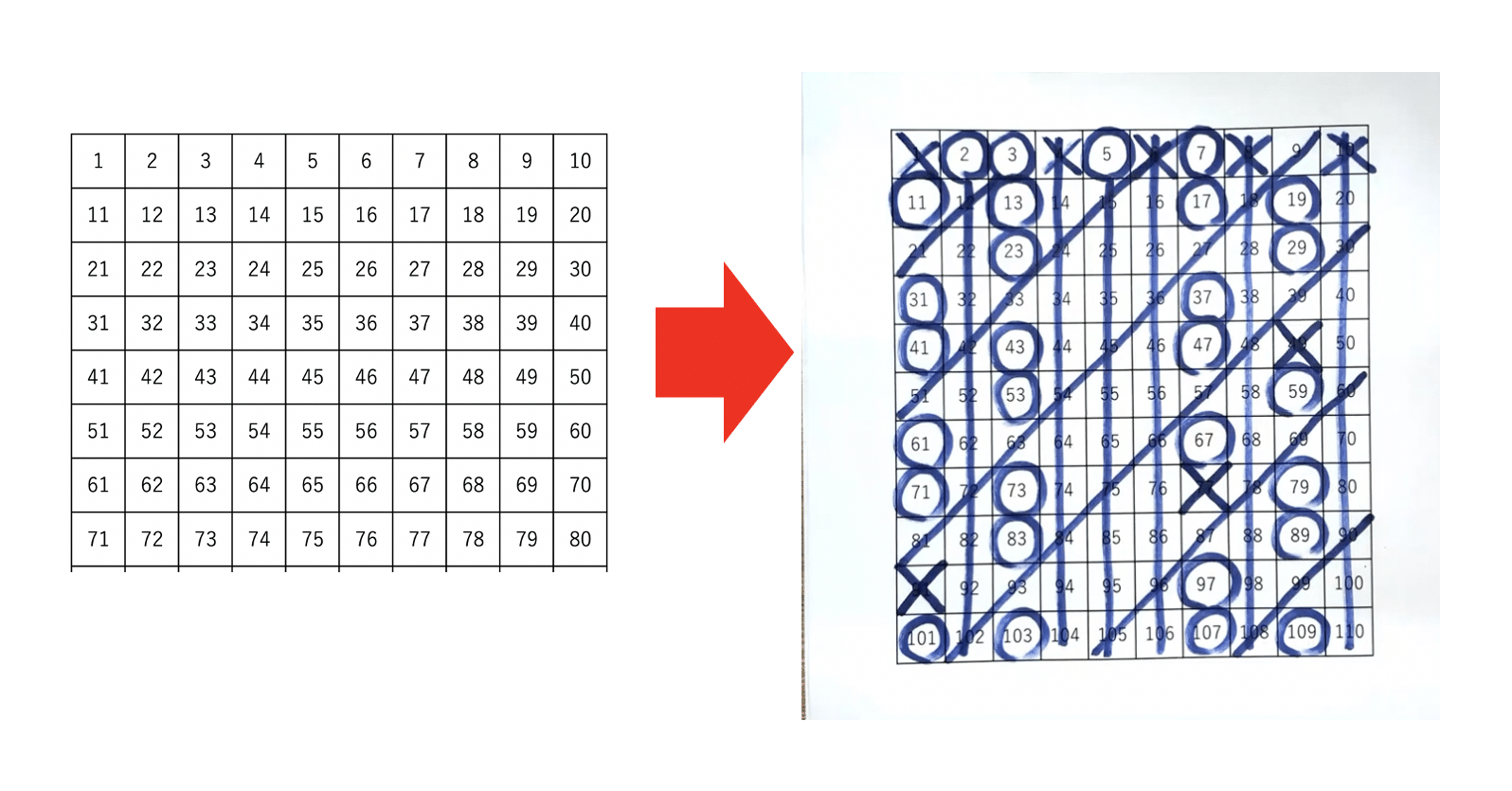
エラトステネスの篩 ふるい で100までにある素数を見つける方法 Math Channel Note

C エラトステネスの篩 ふるい 再び Qiita

19年の素数日 エラトステネスのふるい 情報科 いっぽ まえへ

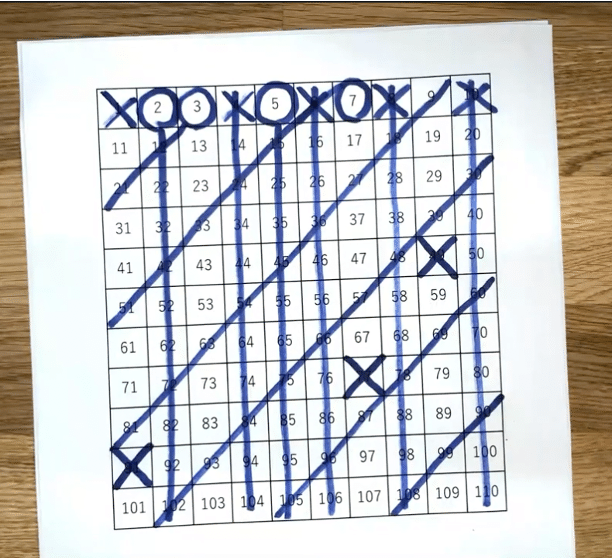
エラトステネスの篩 ふるい で100までにある素数を見つける方法 Math Channel Note

エラトステネスの篩で調べる 素数判定の上限と平方根の関係性 Szarny Io

山岡の地理b準備室 エラトステネスの篩 ふるい

Webで数学 エラトステネスのふるい Webであなたの夢が叶う

素数をすばやく見つける方法 エラトステネスのふるい 数学の面白いこと 役に立つことをまとめたサイト

素数判定法 エラトステネスのふるい Youtube

エラトステネスのふるい スクールプレゼンター用教材 教材 プリント 学びの場 Com

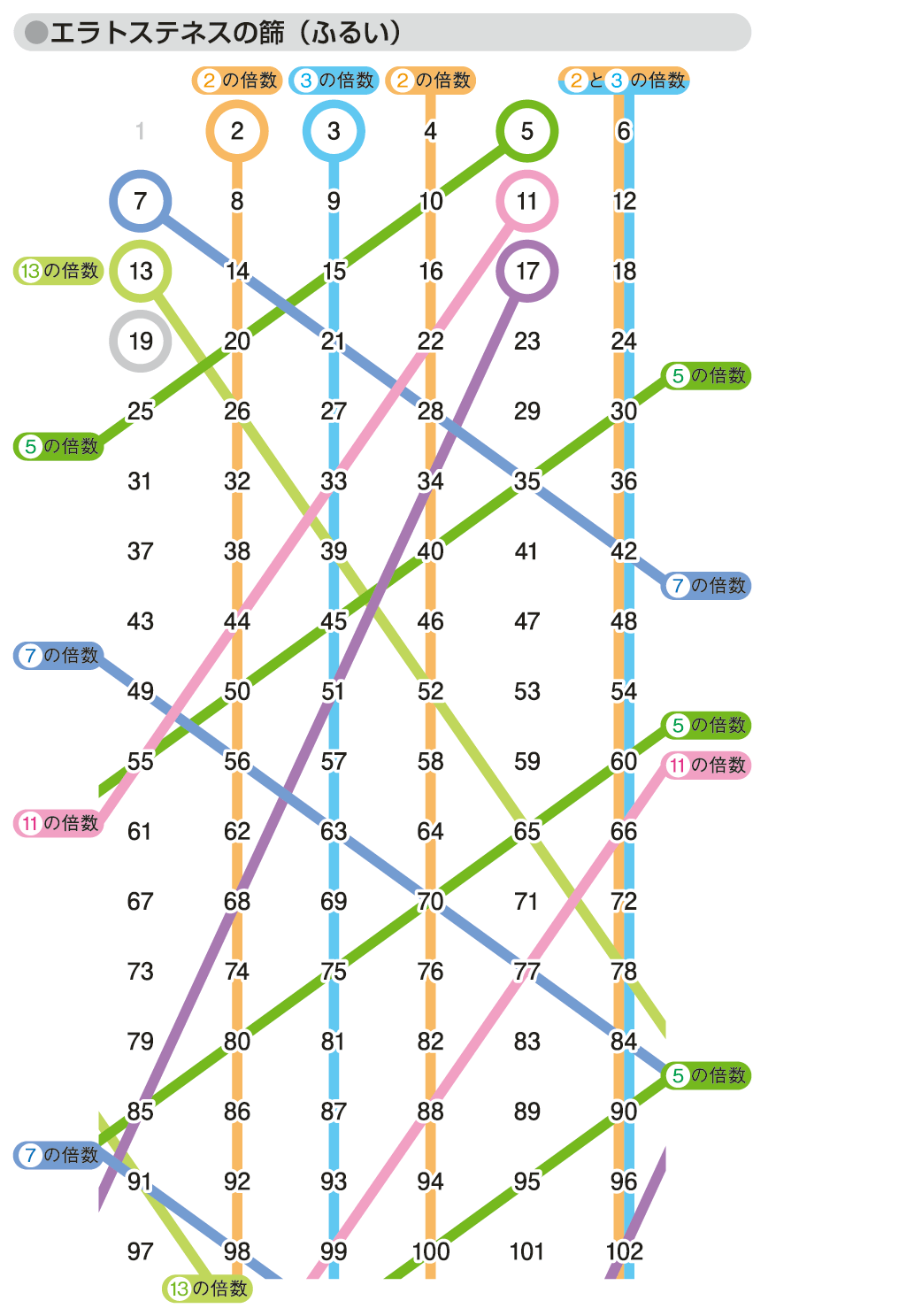
エラトステネスの篩 ふるい 時事用語事典 情報 知識 オピニオン Imidas イミダス

エラトステネスの篩 英丸くんの日常